স্থানের চতুর্থ মাত্রা এবং ডিগা টিগা চিগা
এখন আমরা যা করতে যাচ্ছি তা করার জন্য তিনজনের সাহায্য দরকার হবে। ধরা যাক তাদের একজন ডিগা হচ্ছে দ্বিমাত্রিক প্রাণী, টিগা হচ্ছে ত্রিমাত্রিক প্রাণী, চিগা হচ্ছে চতুর্মাত্রিক প্রাণী। নামগুলো কিন্তু ঠিকমত মনে রাখতে হবে, কারণ ডিগা-টিগা-চিগা পরে আমাদের অনেক কাজে আসবে।
এছাড়া আমাদের আরেকজনকে দরকার হতে পারে। আসলে তাঁকে দরকার নেই(কারণ তিনি মারা গেছেন), তার একটি কথার প্রয়োজন আছে। তিনি বলে গেছেন, “জ্ঞানের থেকে কল্পনা অনেক বেশি গুরুত্বপূর্ণ।“ আর সেই মানুষটি আর কেউ নন, আমাদের অতি পরিচিত আইনস্টাইন। যে কাজটি আমরা করতে যাব, সেখানে জ্ঞানের জায়গা চার আনা, বাকি বার আনাই কল্পনা। তবে যেমন তেমন কল্পনা তো নয়, বলা যেতে পারে যৌক্তিক কল্পনা।
যদি কল্পনা করার ইচ্ছে থাকে তবে শুরু করা যাক ‘সাইকেল না চালিয়ে সাইকেল চালানো শেখা’, আর সঙ্গী হবে ডিগা-টিগা-চিগা!
১.
টিগার সাথে আমাদের সম্পর্ক খুব ভাল, কারণ সে নিজেদের লোক, ত্রিমাত্রিক প্রাণী। আমাদের জগতে স্পেসের
মাত্রা, মানে বাংলায় স্থানের মাত্রা হচ্ছে তিনটি। ত্রিমাত্রিক জগৎ বলতে কি বুঝায় সে ধারনা নিশ্চয়ই সবার আছে, তাই নতুন কোন বর্ণনাতে যাওয়ার দরকার নাই। শুধু জেনে রাখি, আমরা চারপাশে যা দেখি সবকিছুই ত্রিমাত্রিক। কিউব বা ঘনক হচ্ছে ত্রিমাত্রিক বস্তুর খুব সহজ একটি উদাহরণ।
ডিগা দ্বিমাত্রিক প্রাণী। ধরা যাক তার খুবই ইচ্ছে একটা ঘনক দেখা। কিন্তু কাজটা মোটেও সহজ নয়। একজন দ্বিমাত্রিক প্রাণী কখনই ত্রিমাত্রিক বস্তু দেখতে পারবে না।
দুই মাত্রার জগত হচ্ছে অনেকটা কাগজে আকা ছবির মতন। আমরা মাটি দিয়ে কিংবা প্লাস্টিক দিয়ে একটা কিউব বানাতে পারি। কিন্তু কিউব থাকার জন্য দরকার ত্রিমাত্রিক স্থান, দ্বিমাত্রিক স্থানে তার জায়গা কেমন করে হবে? ধরা যাক ডিগার দ্বিমাত্রিক জগত একটি ত্রিমাত্রিক কিউবকে কোনভাবে ছেদ করছে। তাহলে কিভাবে ছেদ করছে তার উপর নির্ভর করে ডিগা কেবল একটি দ্বিমাত্রিক আকৃতি দেখতে পারবে, কিন্তু সত্যিকার অর্থে কিউবটি দেখার ক্ষমতা তার নেই। কারণ একটি কিউবের ছয়টি সমতল পৃষ্ঠ আছে, প্রতিটিকে একটি আলাদা আলাদা দ্বিমাত্রিক বস্তু বলা যেতে পারে। কিউবটি বুঝতে হলে একসাথে একাধিক দ্বিমাত্রিক বস্তুকে দেখতে পারার ক্ষমতা থাকতে হবে, সেটা ত্রিমাত্রিক প্রাণী অর্থাৎ টিগার আছে, দ্বিমাত্রিক প্রাণী ডিগার নেই।
কিন্তু তাই বলে কি ডিগা কিউব কেমন বুঝতে পারবে না? একটা উপায় অবশ্য আছে। দ্বিমাত্রিক জগতে ত্রিমাত্রিক বস্তু থাকতে পারে না। কিন্তু ত্রিমাত্রিক বস্তুর ছবি আমরা কাগজে ঠিকই আঁকতে পারি। ধরা যাক ডিগাকে বুঝানোর জন্য টিগা দ্বিমাত্রিক জগতে কলম দিয়ে একটা কিউবের ছবি এঁকে দিল। খুবই সহজ একটা ছবি, আমরা সবাই কোন না কোন সময় এই আকৃতিটি নিশ্চয়ই বানিয়েছি।
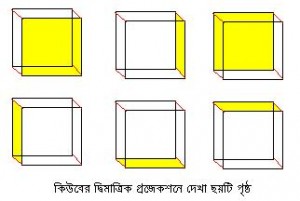
এই ছবিটিকে বলা যায় দ্বিমাত্রিক তলে কিউবের প্রজেকশন। নিচে প্রতিটি তল আলাদা আলাদা রঙ করে দেখানো হল। ডিগাকে কেবল কল্পনা করে নিতে হবে প্রতিটি তল আলাদা আলাদা দ্বিমাত্রিক জগতকে স্পর্শ করতে পারে।
ভাল করে লক্ষ করলে দেখা যাবে যে ঘনকের কেবল দুটি তলকেই বর্গাকার মনে হচ্ছে। ডিগার কাছেও তাও মনে হওয়ার কথা, একটি তল হয়তো তার নিজের জগতে আছে, আরেকটি তার নিজের জগতের সমান্তরাল কোন জগতকে ছুঁয়ে আছে। বাকি তলগুলো দেখতে মোটেও বর্গাকার মনে না হলেও আমরা কিন্তু কল্পনাতে ঠিকই দেখতে পারি অন্য কোন দ্বিমাত্রিক জগতে থাকা প্রাণীর কাছে সেগুলোকে দেখতেও বর্গাকার লাগছে।
২.
চিগা চতুর্মাত্রিক প্রাণী। এবার একটু সতর্ক হওয়া প্রয়োজন। এখানে যে চতুর্থ মাত্রার কথা বলা হচ্ছে তা কিন্তু সময় নয়। এখানকার চতুর্থ মাত্রা স্পেসেরই চার নম্বর একটি মাত্রা। কিন্তু সেই জিনিসটা কেমন আবার?
ধরা যাক ত্রিমাত্রিক প্রাণী টিগার কাছে তিনটি কাঠি আছে। দুটো কাঠি নিয়ে সে টেবিলের উপর এমনভাবে রাখল যেন তারা একে অপরের সাথে লম্বভাবে থাকে। ধরা যাক কাঠি দুটি হচ্ছে A এবং B এবং তারা ছেদ করে O বিন্দুতে।
এখন তিন নম্বর কাঠিটি যার নাম ধরা যাক C, সেটিকে O বিন্দুতে A ও B এর সাথে লম্বভাবে দাড়া করানো হল। কাঠি তিনটিকে যদি তিনটি সরলরেখা হিসেবে চিন্তা করি তাহলে বলা যায়, তিনটি সরলরেখার যে কোন দুটি নিলে তারা একে অপরের উপর লম্ব হবে।
এখন আরেকটি কাঠি দিয়ে যদি টিগাকে বলা হয়, অন্য তিনটি কাঠির সাথে লম্ব হবে এমনভাবে এটিকে রাখার ব্যবস্থা কর, সে কি পারবে?
না টিগা পারবে না। কারণ দ্বিমাত্রিক জগতে একটি বিন্দু দিয়ে যেমন কেবল মাত্র দুটি পরস্পর লম্ব সরলরেখা আঁকা যায়, ত্রিমাত্রিক জগতে তেমন তিনটি সরলরেখা আঁকা যাবে। কিন্তু চারটি পরস্পর লম্ব সরলরেখা ত্রিমাত্রিক জগতে থাকতে পারে না।
এখন ওই কাঠিটি চিগার হাতে দিয়ে তাকে যদি রাখতে বলা হয়, সে কিন্তু এমনভাবে রাখতে পারবে যেন অপর তিনটির সাথে চার নম্বরটি লম্বভাবে থাকে। কারণ চিগা চতুর্মাত্রিক প্রাণী, চতুর্মাত্রিক জগতে একটি বিন্দু দিয়ে চারটি লম্ব সরলরেখা আঁকা যেতে পারে! ব্যাপারটা অনেকটা এরকম, চিগা এমন একটি দিকে চলাফেরা করতে পারে যে দিকটি দেখার ক্ষমতা টিগার নেই, ডিগার থাকা তো দূরের কথা।
ডিগাকে কিউব দেখাতে গিয়ে টিগার হঠাৎ চতুর্মাত্রিক হাইপারকিউব দেখার ইচ্ছে হল (হাইপারকিউব এই আকৃতিটির সাধারণ নাম। একমাত্রিক হাইপারকিউব হচ্ছে একটি যে কোন রেখাংশ, দ্বিমাত্রিক হাইপারকিউব হচ্ছে বর্গ, ত্রিমাত্রিক হাইপারকিউব হচ্ছে আমাদের অতি পরিচিত ঘনক বা কিউব)। দ্বিমাত্রিক জগতে কিউবের যেমন প্রজেকশন থাকতে পারে, ত্রিমাত্রিক জগতে হাইপারকিউবের(এখন থেকে হাইপারকিউব বললে আমরা বুঝব চার মাত্রার হাইপারকিউব) তেমন প্রজেকশন আছে। কিন্তু তেমন প্রজেকশন বানানো আমাদের জন্য মোটেও সহজ কাজ নয়(ধরা যাক চিগা খুবই বদমাশ এবং টিগাকে কোন প্রকার সাহায্য করতে রাজি নয়)। তাহলে কি করা যায়?
এবার যে কাজটি আমরা করতে যাচ্ছি সেটি একটি যুগান্তকারী কাজ বলা যেতে পারে। হাইপারকিউবের ত্রিমাত্রিক প্রজেকশন আমরা বানাতে না পারি, হাইপারকিউবের ত্রিমাত্রিক প্রজেকশনের দ্বিমাত্রিক প্রজেকশন তো আমরা খুব সহজেই এঁকে ফেলতে পারি!
কাজটা করা খুবই সহজ। আমরা কাগজে প্রথমে দুটো বর্গ এঁকে তার কোণাগুলো যোগ করে কিউবের ছবি এঁকেছিলাম। এখন কাগজে দুটো কিউবের ছবি এঁকে কোণাগুলো যোগ করে হাইপারকিউবের ছবি আঁকব।
কিউবের ছয়টি দ্বিমাত্রিক পৃষ্ঠ থাকে। হাইপারকিউবের তেমন আটটি ত্রিমাত্রিক পৃষ্ঠ আছে! ডিগার কাছে কিউবের প্রজেকশন দেখে যেমন কেবল মাত্র দুটো পৃষ্ঠকেই বর্গাকার মনে হয়েছিল, হাইপারকিউবের প্রজেকশনের প্রজেকশন দেখে আমাদেরও তেমন কেবলমাত্র দুটো পৃষ্ঠকেই কিউবের মতন মনে হবে। আর কল্পনা করে নিতে হবে অন্য কোন ত্রিমাত্রিক জগতে থাকা প্রাণীর কাছে অন্য যে কোন দুটো পৃষ্ঠ দেখতে কিউব কিউব লাগছে।
সবগুলো কিউব বুঝতে পারার ক্ষমতা আছে কেবল চিগার। সে কেমন করে দেখতে পায়, তার ব্যাখ্যা হয়তো একজন চতুর্মাত্রিক চক্ষু বিশেষজ্ঞই দিতে পারেন।
৩.
চতুর্মাত্রাকে বুঝার জন্য প্রজেকশনই একমাত্র উপায় নয়, অন্যান্য উপায়ও আছে। ডিগা-টিগা-চিগাকে নিয়ে একটি ছোট্ট খেলা খেলে দেখা যাক।
ধরা যাক কোন দ্বিমাত্রিক তলের উপর একটি নিরেট গোলাকার কয়েন রাখা আছে, আর একটি গোলাকার ক্ষেত্র আছে যেটা অনেকটা ফাঁপা বলা যেতে পারে। অর্থাৎ গোলাকার ক্ষেত্রের পরিধি ডিগার কাছে দেয়ালের মত, একে ভেদ করে যাওয়ার ক্ষমতা তার নেই। এখন ডিগাকে বলা হল কয়েনটিকে গোলাকার ক্ষেত্রের মাঝে নিয়ে যেতে।
এই কাজ করা ডিগার পক্ষে একেবারেই সম্ভব না। কারণ দেয়াল ভেদ করে যাওয়া তার পক্ষে যেমন সম্ভব না, ওই কয়েনটিকে দিয়েও দেয়াল ভেদ করানোর ক্ষমতা তার নেই। কিন্তু টিগাকে যদি কাজটি দেওয়া হয়? সে খুব সহজে কয়েনটিকে তুলে নিয়ে অন্য কোন দ্বিমাত্রিক জগতে নিয়ে যেতে পারবে যেখানে দেয়ালের বাঁধা নেই, এরপর সেখান থেকে কয়েনটিকে নামিয়ে আবার ডিগার দ্বিমাত্রিক জগতে এনে সেই গোলাকার ক্ষেত্রটির মাঝখানে রেখে দিতে পারবে। বুঝার সুবিধের জন্য আমরা ধরে নেই যে যখন ডিগার দ্বিমাত্রিক জগতে কয়েনটি থাকে তখন তার রঙ হলুদ, অন্য দ্বিমাত্রিক জগতে নিলে তার রঙ বদলে যেতে থাকে। সুতরাং বিষয়টা দেখতে হবে অনেকটা এই ছবির মত।
এখন ধরা যাক একটি ফাঁপা ত্রিমাত্রিক গোলক এবং আরেকটি নিরেট ত্রিমাত্রিক গোলক টিগাকে দিয়ে বলা হল নিরেট গোলকটিকে ফাঁপা গোলকের ভিতর ঢুকাতে। যথারীতি এই কাজ টিগা করতে পারবে না। কিন্তু যদি চিগাকে বলা হয়?
চিগা খুব সহজে নিরেট গোলকটিকে অন্য ত্রিমাত্রিক জগতের মধ্য দিয়ে নিয়ে ফাঁপা গোলকের ভেতর ঢুকিয়ে দিতে পারবে, তার কাছে কাজটা হবে যেন টেবিল থেকে কিছু উঠিয়ে অন্য কোন জায়গায় নিয়ে রাখার মত, এর বাইরে কিছুই না!
আমাদের ভাগ্য ভাল যে আমাদের আশেপাশে কোন চতুর্মাত্রিক চোর নেই। তাহলে তারা এতটুকুও ঘাম না ঝরিয়ে আমাদের ঘরের সিন্দুক খালি করে দিতে পারত, কিন্তু বসে বসে আঙুল চুষা ছাড়া আমাদের আর কিছুই করার ক্ষমতা থাকত না!
.png)